量子物理学分野

　ニューラルネットワークは、生物の脳をモデル化した関数で、近年効率的な学習を行わせる方法が分かってきました。当研究室では、このニューラルネットワークがどのように自然科学の現象を理解しているのかを調べ、自然科学研究に応用する方法を探求します。

• 研究室ホームページ

教員

小暮 兼三 ( Kenzo OGURE )

助教（工学研究科）

研究テーマ

現在の研究テーマ

• ニューラルネットワークによる自然科学の理解

過去の研究テーマ

• 素粒子と宇宙: 初期宇宙と素粒子（バリオン数生成、ダーク マター）、有限温度場の理論、ニュートリノ振動
• 場の理論におけるソリトン: トポロジカルソリトン、ノントポロジカルソリトン
• ランダム系と情報理論: スピングラス、レプリカ法、情報理論への統計的手法の応用

連絡先

桂キャンパス C3棟 d1S02号室
TEL: 075-383-3909
FAX: 075-383-3909
E-mail:ogure.kenzo.8v@* (スパム対策のためメールアドレスを省略しております。@の後にはkyoto-u.ac.jpを追加して下さい。)

研究テーマ・開発紹介

ニューラルネットワークによる自然科学の理解

　ニューラルネットワークがどのように自然現象を理解しているのかを調べ、逆にニューラルネットワークを使って自然現象の理解を進める方法を探索します。

　手法は理論物理学に根ざしたものを用いて、理論と数値実験により行います。計算機以外の装置を使った実験を行う予定はありません。

　研究対象は、量子物理学を含めた物理系を中心としますが、生物のDNA, RNAの塩基配列など自然科学一般としています。

• 動機

　ニューラルネットワークは、生物の脳が学習し、思考する様子をモデルとして研究が進められた計算手法です。具体的にはシナプスを簡単な活性化関数で表現し、それを並列して合成関数を作ることで実装しています。

• 成功の兆しがある

　ニューラルネットワークは、まだ人間の思考をすべて再現できているわけではありませんが、分野によってはすでに人間を遙かに超える能力を発揮しています。特に、2014年に相次いで登場した生成モデルVariational AutoEncoder(VAE)、Generative Adversarial Network(GAN)以来、発達の速度を速めているようです。

　また、離れた層の結合やアテンション機構の導入など、学習を速める工夫も進んでいます。さらに、GPUの高性能化もニューラルネットワークに力を与えています。

　すでに、CHATGPTなど、かなり高度な実用化もなされています。次にCHATGPT4（2024.3.9時点）を用いた生成例を挙げてみます。

「ニューラルネットワークは、人間の脳を模倣した人工知能技術の一種です。複数の層からなるこのシステムは、入力（例えば画像やテキスト）を受け取り、各層で情報を処理し、最終的に出力（例えば識別結果や予測）を生成します。ニューラルネットワークは、学習を通じてデータからパターンを学び、さまざまなタスクでの意思決定や予測を改善します。この技術は、画像認識、自然言語処理、予測分析など、多くの分野で応用されています。」

• 数学・物理学的な見方

　ニューラルネットワークは、数学的に見るとm次元の実数を入力とし、n次元の実数を出力とする関数です。この関数には、ニューロン間をつなぐ係数に当たる多くのパラメーターが含まれています。

　ニューラルネットワークの学習は、物理学的に見ると、この関数に含まれる多くのパラメーターを出力がなるべく正しくなるように調整する変分法と考えられます。

• 理解の兆候

　ニューラルネットワークは、ただデータを丸覚えしているだけはなく、人間の理解と近いと思われる傍証があります。例えば、VAEであれば潜在空間に自然に特徴量を取り出していますし、転移学習であればある分野で学んだことを他分野に活かしています。この特徴は、自然科学を研究するために必要な要素となります。

• 変分関数

　ニューラルネットワークを変分関数として見た場合、物理学で通常使われる変分法に比べて、2つの大きな特徴があります。

1. 関数型：物理学における変分法では、通常、境界条件や物理的直感によって関数型を仮定し、パラメーターの数をなるべく減らすようにします。一方、ニューラルネットワークにおいては、汎用の活性化関数を用います。
2. パラメーター数：ニューラルネットワークでは数百万を超える多数のパラメーターを含むこともあり、汎用の活性化関数しか用いなくても、柔軟な表現を可能にしています。

　上の2つの特徴により、ニューラルネットワークは自然科学の研究において、大きな可能性を秘めていると言えます。自然科学においては、慣例的に使われてきた常に正しいとは言えない近似や変分関数の形があります。多くの場合、こういった仮定は、解析的に問題を解くためであったり、現実的な時間で数値計算を終えるために導入されますが、ニューラルネットワークは、このような仮定を必要としないので、先入観のない研究を行うことができると期待されます。将棋や囲碁をされる方は、AIが示す最善手がとても人間では考えつかないようなものである場面を多々見られていると思います。

　汎用の活性化関数を用いても高い精度の予測を行うことができる原動力は、主にパラメーターの多さが担っており、ニューラルネットワークは非常に柔軟な表現が出来る関数と捉えられます。必ずしも正しいたとえではないですが、「猫らしさ」といった概念が物体のようなものだとイメージすると、柔軟な粘土をそこに押し当てて、型を写し取っているような感覚かもしれません。

• 新しい技術である

　ニューラルネットワークの実用的な大きな発展は、2014年以降に行われており、まだまだ試されていない事ばかりです。また、日進月歩でニューラルネットワークの構成法自体も進化しており、新しい結果が出しやすい分野であると思われます。

• 研究対象が広い

　ニューラルネットワークが、画像・音声・動画・言語などいろいろな分野で多様な利用がされていることからも分かるように、適用範囲が広いです。自然科学のほとんどの問題は、m次元の実数からn次元の実数への写像問題に焼き直すことが出来ますので、物理学に限らず、化学、生物、地学、医学などあらゆる自然科学の研究に利用できると考えられます。

• 環境が整いつつある

　ニューラルネットワークの有望性が確認されつつある中、ニューラルネットワークをPythonで簡単に作成できるライブラリーが提供・更新され続けています。また、GPUも日々高性能化しており、ニューラルネットワークを用いた自然科学の研究を行う環境は整いつつあります。

• ニューラルネットワークは理解しているのか

　ニューラルネットワークは、分野によっては人間以上の出力を行うことは分かってきましたが、ニューラルネットワークが物事を理解していると言えるのかや、その理解の形態はどのようなものかは、自明ではありません。その理由は、ニューラルネットワークの学習結果は、多数のパラメーターに埋め込まれており、物理学における運動方程式やシュレディンガー方程式、分配関数のような統一的な理論が示されるわけではないためです。

　変分法として捉えた場合も、物理学における伝統的な変分法であれば、変分関数自体が現象論的な寄与を足し合わせたような形で書かれていることが多いので、どの係数が大きくなっているかである程度の状況を読み取れますが、ニューラルネットワークではそのようなことが出来ません。

• 自然科学においては理解が重要

　しかし、ニューラルネットワークの理解を読み取ることが不可能というわけではありません。活性化しているニューロンの観測や入力の変化に対する応答を見ることで、ニューラルネットワークがどのように物事を理解しているのかを推定する事が出来ます。自然科学においては、統一的な法則の理解や予言能力が重要になってくるので、ニューラルネットワークの理解について探求することには深い意味があります。

• ニューラルネットワークの理解を確かめる数値実験

　ニューラルネットワークが自然科学を理解できているかを確かめるために当研究室で行った数値実験を紹介します。物理系は、1次元の量子力学で、入力はランダムに生成されたポテンシャルのグリッド上での値とし、出力はエネルギースペクトルの低いものから10個としました。

論文

"Observing how deep neural networks understand physics through the energy spectrum of 1D quantum mechanics," Kenzo Ogure, Progress of Theoretical and Experimental Physics, Volume 2022, Issue 11, November 2022

• エネルギースペクトルをほぼ正確に再現

　入力をポテンシャルのグリッド上の値とし、出力をエネルギースペクトルの低いものから10個の値として、ニューラルネットワークを学習しました。

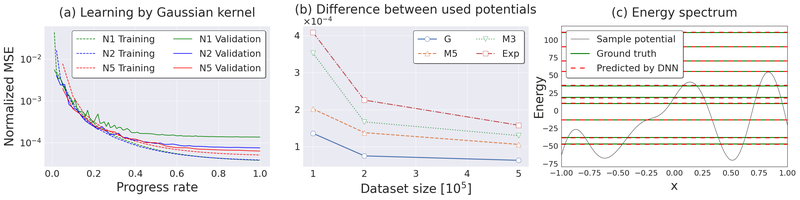
　一番左の図は、学習が進捗すると損失が小さくなっていることを表しています。真ん中の図は、入力データの多様性を増すと損失が小さくなっていることを表しています。一番右の図は、エネルギースペクトルがほぼ再現されていることを示しています。

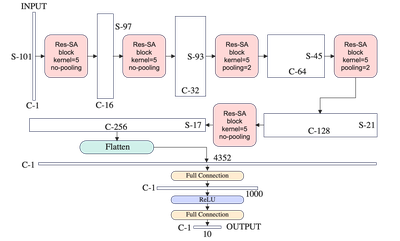
　ニューラルネットワークの全体図です。500万個くらいのパラメーターを含んでいます。

• ニューラルネットワークは物理法則を理解していた

　ニューラルネットワークが物理法則を理解していることを確かめるために、ニューラルネットワークに与えていない量を引き出すことを考えました。具体的には、ポテンシャルとエネルギースペクトルは与えていましたが、波動関数は与えていなかったので、波動関数をニューラルネットワークが知っているかどうかを確かめました。

　ニューラルネットワークは、パラメーターや入力に関する微分をバックプロパゲーションという方法で簡単に計算できるので、エネルギー固有値の入力データに関する微分を計算しました。この量は、ニューラルネットワークが正しくこの物理系を理解していれば、そのエネルギー固有値に対する波動関数の大きさの2乗になるべき量です。

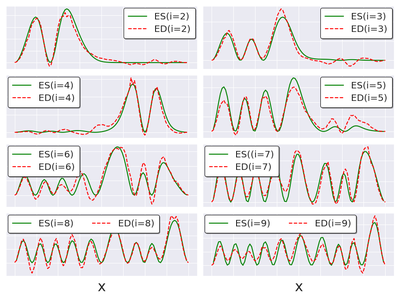
　このグラフから分かるように、10個の波動関数をほぼ正しく再現していることが分かります。この事実から、ニューラルネットワークはただデータを覚えただけではなく、その裏側にある量子力学の理論を理解していたことが分かります。

• 物理現象を再現

　ニューラルネットワークが物理現象の予言を出来ることを示すために、学習したニューラルネットワークを用いて数値実験を行いました。具体的には、1次元の量子力学にはエネルギー固有値の縮退が無いことを確かめました。これは、アンモニア分子のエネルギースペクトルを観測することでも確かめられる物理現象でもあります。数値計算上は、2つの異なるポテンシャル間を連続的に変化させ、エネルギー固有値がどのように変化するかを調べました。

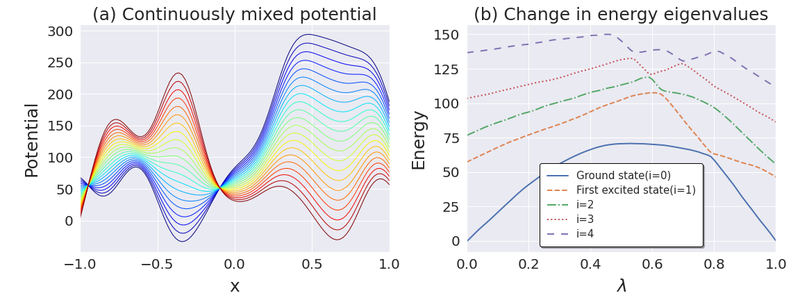
　左の図は、2つのポテンシャルをつなぐように連続的に生成したポテンシャルであり、右の図はエネルギー固有値の変化です。縮退することなく乗り換えが行われていることが分かります。この現象は、実際の物理でも太陽ニュートリノ振動のMSW効果などで知られています。

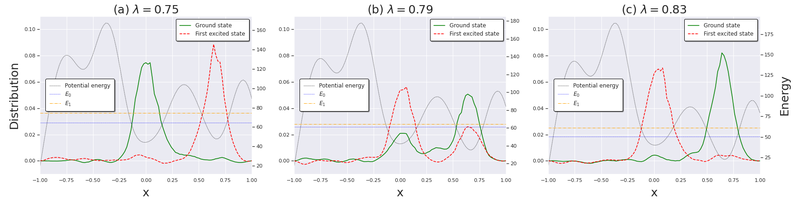
　エネルギー固有値が接近する付近での波動関数の乗り換え挙動も再現されています。

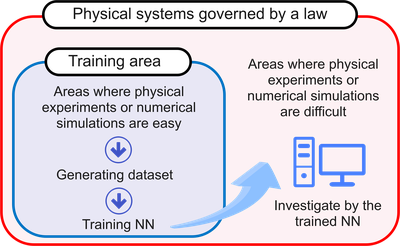
• ニューラルネットワークが自然科学の法則を理解するのであらば、適用範囲が広がる
  

　ニューラルネットワークが自然科学の法則そのものを理解できるのであれば、いろいろな応用が考えられる。例えば、実験でデータを得やすいパラメーター領域のデータを用いてニューラルネットワークを学習し、法則を理解したニューラルネットワークを用いて実験が行いにくいパラメーター領域の実験結果を予測することも出来る。

• 原則として各学年で1名とさせてください

　当研究室に所属していただく方法は、原子核工学コースの4回生がグループ配属時に希望する方法と、大学院入試を受けて頂く方法があります。大学院入試の場合、原子核工学専攻では合格すれば、好きなグループに配属を希望することが出来ます。

　ところが、現実には当研究室は小暮一人で指導しており、理論の研究室としての原子核工学コース・専攻での役割分担や、研究室の事務作業も行っています。また、理論のテーマは物や手法を少しずつ変えて与えるということも難しく、出てきた結果を見て、臨機応変に方向を修正していく必要があります。そのため、多くの学生を指導する事が出来ません。大学院入試の制度とは矛盾してしまうのですが、学生さんのためにも原則として配属は学年で0名か1名でお願いしたいと考えています。

• 当研究室での研究に必要な素養

　当研究室は、理論物理学の手法を用いて、ニューラルネットワークによる自然科学の理解を調べるというテーマで研究を行っており、配属される学生には以下の素養が必要になります。

直接的に必要な素養

解析学、確率論、統計力学

間接的に必要な素養

数学（線形代数、複素解析）、物理学（力学、解析力学、熱力学、電磁気学、量子力学）

　また、自然科学一般の現象に興味を持って、腰を落ち着けて、原理から深く各現象を理解したいと思われる方が向いていると思います。最新のキーワードに敏感で、ブルーバックス的な知識を広く多く集めて、うまくミックスしていきたいというタイプの方は向いていないかと思います。もちろん、そういう方を求められている研究室も多くあると思いますし、方向性が違うだけだと思います。

• 配属を希望する場合は、必ず面談をお願いします

　原子核工学コース・専攻では、配属の際に事前の面談を要求していないのですが、当研究室を希望される場合は、受け入れ能力が限られているので、大変申し訳ないのですが、必ず面談を受けてください。手順は、以下の要領でお願いします。

1. メールで所属・成績表をお送りください。メールアドレスは上にあります。
2. 成績に問題なければ、日程を調整します。直前では対応できませんので、1ヶ月以上の余裕を持ってご連絡ください。
3. 面談では、受け入れ可能性や進路について、フランクにお話したいと思います。なお、大学院入試の問題や要領については、規定により一切お答えできませんので、その点はあらかじめご了解ください。

• 必要とされる成績の目安

　大学院入試の過去問や合格実績を見て頂ければ分かるように、原子核工学専攻の大学院入試は驚くほど簡単です。協力講座の影響で、学部の定員より大学院の定員の方が多くなっているのが一つの事情になっています。大学を留年して卒業する方でも、ほぼ合格しています。

　しかし、理論的な研究はこの大学院入試に合格できたというだけでは難しく、当研究室に配属されてしまったばかりに、自力での卒業・修了が難しくなることがよくあります。

　理論物理の研究室を志望する目安はどこでもあまり変わらないと思いますが、数学（解析学、線形代数、複素解析）と物理（力学、解析力学、熱統計力学、電磁気学、量子力学）のほぼすべての教科がAかA+か80点以上で合格していることだと思います。当研究室の面談を受けられる方は、これを一つの基準としてください。ほかの教科の成績は問いませんが、英語はある程度出来た方よいと思います。

　なお、成績の目安や面談は明文化されている基準や規定ではなく、当研究室からの切なるお願いであって、無理をすれば自由に大学院入試を受けて、配属希望を出すことは出来てしまいます。